In this post, we'll figure out how to create a bitcoin address from scratch.

Contents

• Generating Entropy
• Mapping Entropy to BIP39 Words
• Elliptic Curve Cryptography Basics
• Finding the Point, or Public Key
• From Public Key to Address
• From Private Key to WIF
• Conclusion

Generating Entropy

Entropy, in the thermodynamic sense, relates to the available energy a system has that can do be transformed into heat or useful work. A system with low entropy is very ordered, and it's energy is very available; a system with high entropy is very unordered, and it's energy is very unavailable.

Entropy, in the cryptographic sense, is the measure of how unpredictable a sequence of bits is. In our case, we want random, high entropy private key, so much so that guessing it is astronomically, almost physically, impossible.

The first step is to generate the entropy for the private key. To do this, we need a source of random data. The best way to do this is to sample random/chaotic events, like electromagnetic radiation, a noisy microphone, or radioactive decay. The linux kernel uses device timings, and keyboard/mouse input as entropy sources for /dev/random. You could flip a coin just as well; we'll use dice throws 🎲.

To create a key with enough entropy (ie: hard to guess), we want around 256 bits. Since a dice has 6 possible values, a single throw contributes log2 6 = 2.58 bits of entropy, so we'll do 100 throws to get a little over 256 bits. You should get something like this:

1542263214
2451632542
1341224566
1452214365
4632152465
2345126456
2314516421
2134514621
1645164216
2146516424

---

Mapping Entropy to BIP39 Words

Ok, so how do we go from 100 digits to 24 words? Here's the process:

First, calculate the SHA256 hash of this number:

from hashlib import sha256

entropy = '1542263214245163254213412245661452214365463215246523451264562314516421213451462116451642162146516424'

digest = sha256(entropy.encode()).hexdigest()

'''
cd2ea5df3ecccad86ea9d41c9418cb302ad6e219f20561d10bee3a806ffb93c8
'''

Then convert the hex digest into binary:

digest = 'cd2ea5df3ecccad86ea9d41c9418cb302ad6e219f20561d10bee3a806ffb93c8'

binary = bin(int(digest, 16))

'''
11001101001011101010010111011111
00111110110011001100101011011000
01101110101010011101010000011100
10010100000110001100101100110000
00101010110101101110001000011001
11110010000001010110000111010001
00001011111011100011101010000000
01101111111110111001001111001000
'''

The BIP39 wordlist has 2048 words, so you need log2(2048) = 11 bits to index a word. With 256 bits, we can make 23 words, with 3 bits remaining. But what about the 24th word?

The last word is a checksum (ie: it depends on the value of the previous 23). This is useful so that you don't enter an incorrect seed by mistake, and also implies that most word combinations are invalid (ie: you can't randomly pick 24 words).

Let's separate the digest bits into 11 bit pieces and get the corresponding words from the wordlist (remember to +1 the numbers below, since the list from the link above is not 0-indexed. ie: 1641 becomes 1642):

 1: 11001101001 -> 1641 -> snake
 2: 01110101001 -> 937  -> inside 
 3: 01110111110 -> 958  -> jelly
 4: 01111101100 -> 1004 -> laugh
 5: 11001100101 -> 1637 -> smile
 6: 01101100001 -> 865  -> history
 7: 10111010101 -> 1493 -> rival
 8: 00111010100 -> 468  -> dentist
 9: 00011100100 -> 228  -> broken
10: 10100000110 -> 1286 -> patch
11: 00110010110 -> 406  -> crazy
12: 01100000010 -> 770  -> gate
13: 10101101011 -> 1387 -> pulp
14: 01110001000 -> 904  -> illegal
15: 01100111110 -> 830  -> guitar
16: 01000000101 -> 517  -> doll
17: 01100001110 -> 782  -> gift
18: 10001000010 -> 1090 -> marriage
19: 11111011100 -> 2012 -> wine
20: 01110101000 -> 936  -> insect
21: 00000110111 -> 55   -> alone
22: 11111101110 -> 2030 -> worry
23: 01001111001 -> 633  -> execute
24: 000________ -> _    -> _

Now, let's calculate the checksum. We have the bits 000 left from our process; we need 8 more to make 11. To do that, we hash our entropy digest from above with SHA256 again. Then we get the first byte of this new digest and append them to the sequence:

digest = 'cd2ea5df3ecccad86ea9d41c9418cb302ad6e219f20561d10bee3a806ffb93c8'

digest2 = sha256(bytes.fromhex(digest))

'''
4f91e4a416465d7bbdc7c6dd105aaabfce74fe2c279efdb24902ce16b0fc81e4
'''

The first byte of the new digest is 4F. Converting this to binary, we get 01001111. Appending this to 000 yields 00001001111, or 79, in base10. This corresponds to the word antique in the wordlist. Our BIP39 words will then be:

 1: 11001101001 -> 1641 -> snake
 2: 01110101001 -> 937  -> inside 
 3: 01110111110 -> 958  -> jelly
 4: 01111101100 -> 1004 -> laugh
 5: 11001100101 -> 1637 -> smile
 6: 01101100001 -> 865  -> history
 7: 10111010101 -> 1493 -> rival
 8: 00111010100 -> 468  -> dentist
 9: 00011100100 -> 228  -> broken
10: 10100000110 -> 1286 -> patch
11: 00110010110 -> 406  -> crazy
12: 01100000010 -> 770  -> gate
13: 10101101011 -> 1387 -> pulp
14: 01110001000 -> 904  -> illegal
15: 01100111110 -> 830  -> guitar
16: 01000000101 -> 517  -> doll
17: 01100001110 -> 782  -> gift
18: 10001000010 -> 1090 -> marriage
19: 11111011100 -> 2012 -> wine
20: 01110101000 -> 936  -> insect
21: 00000110111 -> 55   -> alone
22: 11111101110 -> 2030 -> worry
23: 01001111001 -> 633  -> execute
24: 00001001111 -> 79   -> antique

Now, this sequence of 24 words encodes the entirety of our 256 bit private key (with 256 bits of entropy) in a human-readable format.

You can check that you did everything correctly with this utility made by Coinkite: rolls.py.

You might be wondering: isn't the private key 264 bits long, since 24 * 11 = 264? No, because the last 8 bits are derived from the previous 256 bits, so they don't encode any new information. This same principle is used in BIP32 child key derivation: a single, master, private key has the information to create virtually infinite child keys.

---

Elliptic Curve Cryptography Basics

So bitcoin uses this thing called Elliptic Curve Cryptography. Basically, an elliptic curve is a curve described by an equation of this form:

$$y^2 = x^3 + ax + b,$$

where a and b are integers. A curve of this family looks like this:

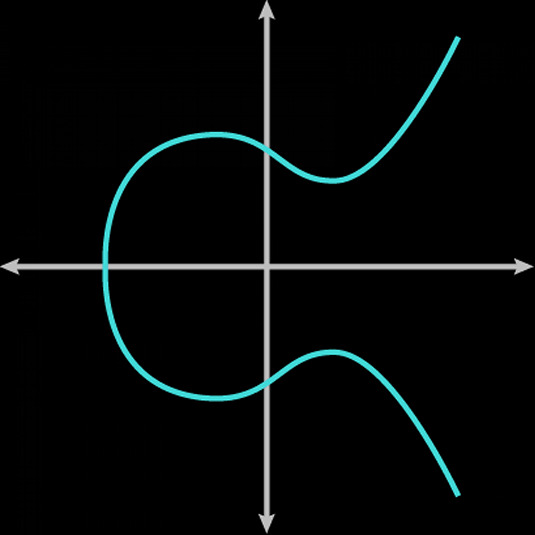
Bitcoin uses an elliptic curve called secp256k1 (full spec here). This basically defines coefficients for the curve, where the Generator point (G) is, and the size of the finite field over which operations are done. They are:

p = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
  = 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1

a = 0x00

b = 0x07

G = 0x0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798 (compressed generator point)

n = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141 (order n of G)

Our EC equation will then be:

$$y^2 = x^3 + 7$$

Since the curve is over a finite field, it ceases being continuous and becomes discrete, like this:

When doing finite field math, all operations are done mod p, so that we don't overflow out of the field.

---

Finding the Point, or Public Key

Okay, so we have our 256 bit private key, and the secp256k1 curve. How do we derive a public key from that?

A public key is just a point on this curve. We get a Public Key point, P, by multiplying the generator point, G, by our private key, k (in our case, k are the 24*11 bits that we derived from our entropy), like this:

$$P = k * G$$

In python, this is done like so:

import coincurve

# field size
p = int('FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F', 16)

# private key derived from dice entropy + checksum
k = \
'''
1100110100101110101001
0111011111001111101100
1100110010101101100001
1011101010100111010100
0001110010010100000110
0011001011001100000010
1010110101101110001000
0110011111001000000101
0110000111010001000010
1111101110001110101000
0000011011111111101110
0100111100100001001111
'''.replace('\n', '')

# convert k to int, keep k inside the field
k = int(k, 2) % p
'21099461583037868212411742703127280085327935027273309817117142164330199307948'

# generator point
G = coincurve.PrivateKey.from_int(1).public_key

# public key point (k*G)
P = G.multiply((k).to_bytes(32, 'big'))

# public key point coordinates on secp256k1
P.point()
'''
(13689447327751707629742410436999816128049105109356453199828972682342657779536,
 110371717352778462288637031811684499582752193961678501703008296578457562351385)
'''

# compressed public key (0x03 + x coordinate)
P.format().hex()
'031e43f3de46ad41ab1ee7d9fbcb8a731169163340e5d31788709d166924396750'

Ok, so from this process we got our public key. How do we transform it into an address?

---

From Public Key to Address

Let's calculate the address corresponding to the public key above. Note that this process will yield a Legacy type address, and not SegWit or Taproot. Below are the steps in python, with pubkey=031e43f3de46ad41ab1ee7d9fbcb8a731169163340e5d31788709d166924396750. Remember to always do the operations on the raw bytes, and not on the hex string.

from hashlib import sha256
from base58 import b58encode
from ripemd.ripemd160 import ripemd160

pubkey = '031e43f3de46ad41ab1ee7d9fbcb8a731169163340e5d31788709d166924396750'

# [1]: Calculate the SHA256 hash of the pubkey
sha256(bytes.fromhex(pubkey)).hexdigest()
'0444b8b3b30fae663f25da3274c1a6f258c55615aad8c56cf5557c6aae7766b1'

# [2]: Calculate the RIPEMD160 hash of the previous hash
ripemd160(bytes.fromhex('0444b8b3b30fae663f25da3274c1a6f258c55615aad8c56cf5557c6aae7766b1')).hex()
'b441f02c6fbd0eb2dfe13b7eb9a839b59ce9ebc3'

# [3]: Prepends version byte 0x00
'00b441f02c6fbd0eb2dfe13b7eb9a839b59ce9ebc3'

# [4]: Calculate checksum: double SHA256 of the previous value, take first 4 bytes
sha256(bytes.fromhex('00b441f02c6fbd0eb2dfe13b7eb9a839b59ce9ebc3')).hexdigest()
'8d9af911d1b967c98f380f1e93bbe4e4f589942fd45c6e877a78692b0a47447b'

sha256(bytes.fromhex('8d9af911d1b967c98f380f1e93bbe4e4f589942fd45c6e877a78692b0a47447b')).hexdigest()
'52aa282f25cd16382f61a18b4d8b498098fa0f430fc19ad5455a85f7e0b1e45b'
 ^^^^^^^^
# checksum
'52aa282f' 

# [5]: Append the checksum to the value from step [3]
'00b441f02c6fbd0eb2dfe13b7eb9a839b59ce9ebc352aa282f'

# [6]: Encode this value to base58
b58encode(bytes.fromhex('00396342b97c4ed295af64f4eabebbd82256c5fef21e9a6a18'))
'1HS7czgBHsRy93JTXfp974mM4G7WPF5xgW'

# [7]: If there is more than one `1` in the front, remove it or them (none in our case)
'1HS7czgBHsRy93JTXfp974mM4G7WPF5xgW'

The address derived from the public key 031e43f3de46ad41ab1ee7d9fbcb8a731169163340e5d31788709d166924396750 is 1HS7czgBHsRy93JTXfp974mM4G7WPF5xgW.

You can now send bitcoin to this address (but you really shouldn't).

---

From Private Key to WIF

Now, let's say you wan't to import this private key to a wallet. You can't just enter it in integer or hex form. Like with the address, we must first hash and transform it, into something called WIF, or Wallet Import Format. It incorporates hashing and and checksums so as to be less error prone when copying it. Here's how:

from hashlib import sha256
from base58 import b58encode

p = int('FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F', 16)

# private key in binary form
k = \
'''
1100110100101110101001
0111011111001111101100
1100110010101101100001
1011101010100111010100
0001110010010100000110
0011001011001100000010
1010110101101110001000
0110011111001000000101
0110000111010001000010
1111101110001110101000
0000011011111111101110
0100111100100001001111
'''.replace('\n', '')

# private key in integer form
k = int(k, 2) % p
'21099461583037868212411742703127280085327935027273309817117142164330199307948'

# private key hexadecimal form
k = hex(k)
'2ea5df3ecccad86ea9d41c9418cb302ad6e219f20561d10bee3a813cfb96d6ac'

# [1]: Prepend version byte 0x80, and append byte 0x01 if the private key corresponds to a compressed pubkey
'802ea5df3ecccad86ea9d41c9418cb302ad6e219f20561d10bee3a813cfb96d6ac01'

# [2]: Calculate double SHA256 hash
sha256(bytes.fromhex('802ea5df3ecccad86ea9d41c9418cb302ad6e219f20561d10bee3a813cfb96d6ac01')).hexdigest()
'4bb387702336dac286085c03889c48d43a08025e8cedecafe2968639d3ca7522'

sha256(bytes.fromhex('4bb387702336dac286085c03889c48d43a08025e8cedecafe2968639d3ca7522')).hexdigest()
'a2d152221565662ae8196fd2484bf6199cceaddbb9b93a6168d873677b4a439c'

# [3]: First 4 bytes are the checksum
'a2d15222'

# [4]: Append the checksum to the value from [1]
'802ea5df3ecccad86ea9d41c9418cb302ad6e219f20561d10bee3a813cfb96d6ac01a2d15222'

# [5]: Encode [4] in base58
b58encode(bytes.fromhex('802ea5df3ecccad86ea9d41c9418cb302ad6e219f20561d10bee3a813cfb96d6ac01a2d15222'))
'KxnPUkZxhqQprt6j3FEwxiT6VLuPpKk9mgc5fe5GNLXg9ctKBjNh'

That's it, KxnPUkZxhqQprt6j3FEwxiT6VLuPpKk9mgc5fe5GNLXg9ctKBjNh is our WIF formatted private key.

This diagram illustrates the byte-to-byte structure of a WIF-encoded private key:

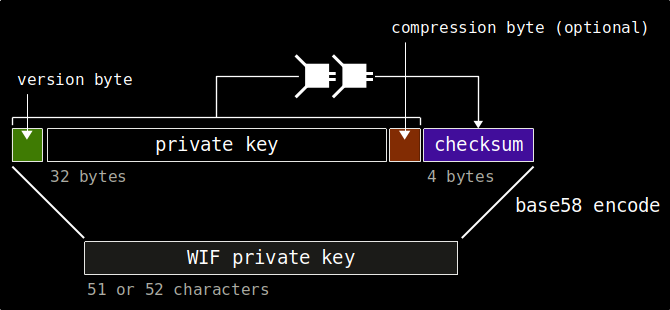
That's it. We have now converted our 256 bit private key into a Wallet Importable Format.

To summarize, we got:

Address -> 1HS7czgBHsRy93JTXfp974mM4G7WPF5xgW

    WIF -> KxnPUkZxhqQprt6j3FEwxiT6VLuPpKk9mgc5fe5GNLXg9ctKBjNh

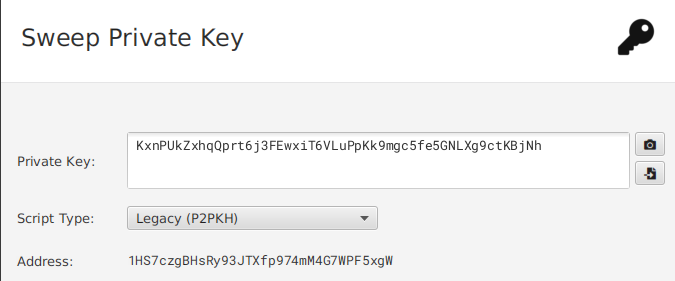
If you try to import this WIF into Sparrow, for example, you see that the address it derives is the same we did:

---

Conclusion

We have generated 256 bits of entropy by hand using dice. Then we mapped this entropy to 24 words, so that it's easier to store our private key. Then we found the corresponding point to our private key on secp256k1. Then we converted this point into an address. Finally, we converted our private key into WIF, a format accepted by wallet software for importing a single private key.